Synchronization and Coupled Oscillators
Spontaneous synchronization.
Numerical simulation with 25 globally coupled (Kuramoto) phase-oscillators.
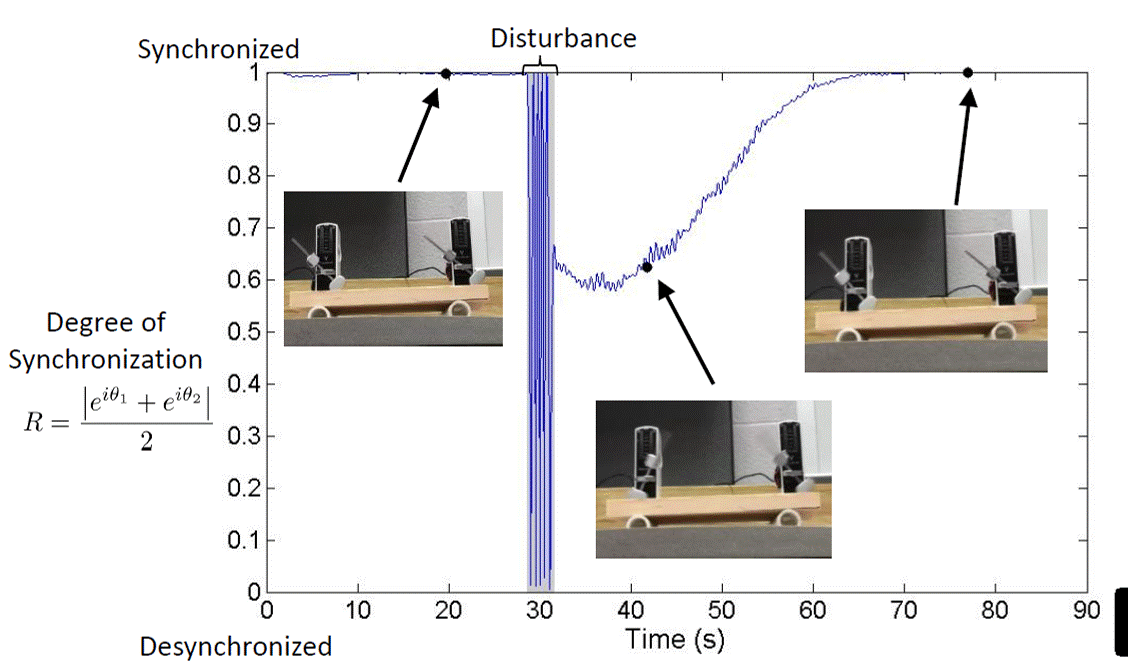
Two metronomes on a sliding platform.
The metronomes spontaneously synchronize after being disturbed. Top: video. Right: recorded data.
Oscillation is a key feature of a host of real-world systems. Cells in the heart contract in a rhythmic manner. Neurons in the brain repeatedly fire and relax. Traffic signals cycle from green to yellow to red and back again. Alternating current is produced by electrical generators and delivered to electrical appliances in buildings around the world.
There are many natural and engineered systems that consist of large numbers of interacting oscillators. When these oscillators are "coupled" together they exchange information about their state and modify their behavior in response to that information. These interactions can lead to unexpected results.
The emergence of synchrony can be desirable or undesirable depending on the circumstances. On a footbridge, synchronized footsteps can lead to dangerous oscillations. While precise synchrony is essential for the efficient operation of telecommunication systems and power generation.
I am interested using mathematical models to identify the conditions and structures that lead to synchrony and the breakdown of synchrony. I am particularly interested in understanding when partially synchronized patterns known as chimera states can stably coexist with synchronized states.