Game theory and vaccination
- Mark J. Panaggio
- Sep 7, 2020
- 11 min read
“What is man that you are mindful of him, and the son of man that you care for him?” – Psalm 8:4
In this Psalm, David ponders this question as he wrestles with just how small and insignificant man is in comparison with God and with the vastness of the universe. His question, “What is man?” is an essential one for social scientists and policy makers to grapple with. Our understanding of man’s nature shapes our view of how man thinks and what he values and therefore how we can predict and govern his behavior.
In economics, human nature is often described using a simplified model sometimes referred to as homo economicus. Homo economicus is a rational being who acts in a “narrowly self-interested” fashion in order to maximize his utility, a concept that represents satisfaction in a broad sense. This means that homo economicus is selfish and cares only about seeking the best outcome for himself. This is not intended to be completely accurate description of human nature, but rather serves as a simplifying assumption that can make otherwise impossible problems tractable. Despite being overly simplistic, it has provided economists with a great deal of insight into how people operate within a society. The field of game theory is arguably one of their greatest successes.
Game theory is the study of the interactions between strategic decision makers. It shows how this self-interested behavior usually leads to mutually beneficial solutions, one of the foundational principles of free market systems. However, it also shows that there are situations where self-interest leads to undesirable outcomes for the group. The most famous example of this is known as the prisoners’ dilemma.
The prisoner’s dilemma goes something like this: Two co-conspirators have been arrested and are being interrogated separately for a serious crime and must decide whether to remain silent or to cooperate with their interrogators. There are four possible outcomes. If both prisoners keep their mouths shut, then the authorities will only be able to charge them with a minor crime. If they both cooperate with the authorities, they will both go away for a long time. However, if one cooperates and the other does not, then the one who cooperates will go free and the other will receive a harsh punishment. The problem is that neither prisoner knows what the other is doing, so they can only base their decision on how they think their co-conspirator will behave. What will the prisoners do?
To illustrate this scenario, it is helpful to describe the various outcomes using a payoff matrix where each pair of numbers represents the utilities of the outcome for each prisoner. The precise numbers don’t matter so much as the relative ordering (the outcome would be the same if you subtracted any constant from each utility), so I will keep things simple and use non-negative numbers to represent the utilities for illustration purposes. The key here is that larger numbers correspond to better outcomes.
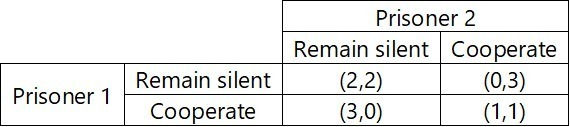
Notice that the best outcome for the group is the one where both remain silent, since the total utility is 4 and the worst outcome is the one where both cooperate since the total utility is 2. Will homo economicus choose the best outcome?
Let’s put ourselves in the shoes of prisoner #1. We must choose between silence and cooperation, but our utility depends on the decision made by our fellow prisoner. If we remain silent, prisoner 2 is better off cooperating since that gives him/her a payout of 3 rather than 2. Similarly, if we cooperate, prisoner 2 is better off cooperating because this gives him/her a payout of 1 rather than 0. So, if prisoner 2 has any sense, they will recognize that no matter what we do, they will be better off cooperating. In light of that, we should assume that if homo economicus is in the other interrogation room, he would cooperate. So we can assume prisoner 2 is going to turn us in. What should we do then? Well, if they cooperate, then we are left with a choice between 0 (remain silent) and 1 (cooperate). So, we are better of cooperating as well.
The remarkable thing about the prisoners’ dilemma is that this argument is symmetrical. Prisoner 2 can make the exact same argument about prisoner 1. Therefore, rational self-interested prisoners would both choose to cooperate and they are both worse off as a result.
The prisoners’ dilemma is a metaphor for all kinds of strategic decisions that involve shared costs by society. For example, if you replace remain silent with “recycle” and cooperate with “pollute”, then this same payoff matrix can be used to show why it is so hard to get people to recycle even if we would all be better off if we did so. Homo economicus recognizes that recycling comes with a personal cost even if there is a benefit to society, so each person is better off if everyone else recycles (keeping the planet clean) and they don’t. This is known as the free-rider problem and it illustrates that sometimes we have a perverse incentive to take the easy road in order to benefit from the sacrifices of others. Because of the free rider problem, many people do not recycle and we are all worse off as a result.
The central lesson that we can take away from the prisoners’ dilemma is that, although acting out of self-interest often produces good solutions for the group, it doesn’t always! Sometimes, self-interest can lead to solutions where everyone is worse off. As we will soon see, this is what occurs when people take a self-interested approach to vaccination.
The strategic elements of vaccination are a bit more complex (for one, there are a lot more players!), but the tools of game theory can still be applied. In weighing the decision to get vaccinated or not, there are a couple of factors to consider:
1. The cost of getting the vaccine. Getting vaccinated takes time and effort. It is inconvenient, unpleasant and may come with a small price tag. Beyond that, there is some small risk of an adverse reaction. Vaccines are generally safe. There is a rigorous testing process in place involving multiple stages of safety trials. The rare exceptions to the adage that vaccines are safe are the result of taking shortcuts and/or ignoring red flags during these trials. As long as the testing process is followed and not rushed, we can expect that unsafe vaccines will be stopped before ever reaching mass distribution. That said, there is always the risk that a small segment of those who are vaccinated experience a negative side effect. In order for a vaccine to be approved, this risk must be substantially smaller than the risk associated with catching the disease the vaccine is intended to catch. So vaccination comes with a cost and unless the benefits are great enough to offset this cost, most would prefer not to get vaccinated. Note: I am not an immunologist. Please consult the CDC or HHS for information about the safety and reliability of vaccines from the real experts.
2. The cost of the infection. This will vary from person to person and will depend on the pathogen being vaccinated against. However, as a general rule, the more severe the infection (i.e. the higher the stakes), the more willing people will be to go to the trouble of getting vaccinated.
Together, these two factors can be represented using a single ratio which I will call the relative cost of infection, c. If c>1, then the cost of being infected exceeds that of getting vaccinated, this means, if c<1, then the cost of infection is less than the cost of getting vaccinated, and if c=1 then those costs are perfectly balanced. In general c will always be greater than 1 for any real world vaccine because that is the only scenario where vaccine development is worth the effort.
There is one additional factor that must be considered when deciding whether to be vaccinated:
3. The probability of getting sick. The probability of getting sick depends on whether you have been vaccinated and how prevalent the pathogen is. This can be estimated using standard epidemic models. However, it is reasonable to assume that this probability will be less than one since not everyone gets sick.
The choice to get vaccinated involves a bit of a gamble. You can get vaccinated and bear the cost of vaccination (which we will define to be 1 without loss of generality). Or you can skip the vaccination and roll the dice that you will not get sick (probability 1-p). If you get sick (probability p), then you bear the cost of infection (c). However, if you do not get sick, then you have no costs at all.
Ultimately, a rational agent such as homo economicus would choose the course of action that has the lowest expected cost. In other words, he would think about which strategy would cost less in the long run if he was able to make the gamble over and over again.
Up to this point, this may not sound anything like the prisoner’s dilemma, but there is an important detail that we have overlooked thus far: the probability that you get sick depends on whether other people get vaccinated. If no one gets vaccinated, then everyone has a high risk of infection. However, when people get vaccinated, not only do they benefit by reducing their risk of infection, everyone else benefits as well because it reduces the probability of infection for everyone else. This is worth repeating: when each person gets vaccinated, the benefits to society exceed the benefits to the individual. Economists refer to this as a positive externality.
This means that what is best for me may not be aligned with what is best for society as a whole. If enough people get vaccinated, then herd immunity will be reached leading to a drastically lower risk for everyone. You can show that the optimal solution for society (i.e. the one with the lowest average cost) is to have just enough people get vaccinated to reach herd immunity. However, vaccination decisions are not made from this top down perspective. People make individual decisions about whether to get vaccinated and their incentives are NOT perfectly aligned with those of society.
In other words, this is a situation where the free-rider problem again rears its ugly head. Each person is best off if everyone else bears the cost (of vaccination) so that they can reap the benefits of herd immunity for free. As a result, you can show that the optimal individual strategy (formally known as the evolutionarily stable strategy) is a “mixed strategy” in which people get vaccinated less often than is required for herd immunity. Rather than getting into the details, let’s look at plot to summarize the implications of this:
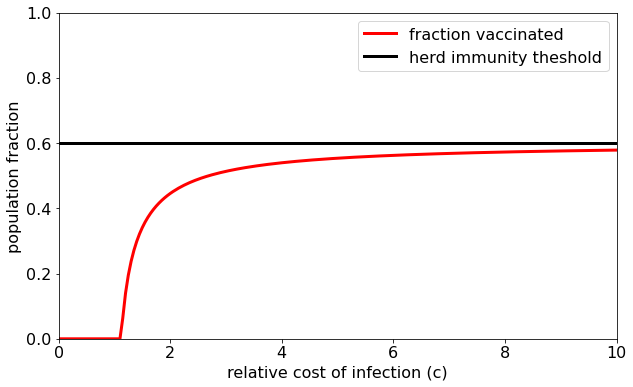
Here the horizontal axis tells us how dangerous the infection is relative to the cost of vaccination. So, if you think about some of the more well-known infectious diseases, Ebola would be way off to the right (very deadly), the 2009 strain of H1N1 (Swine Flu) would be much further to the left but still above 1 (not very deadly if you are healthy), and the 1918 strain of H1N1 (Spanish flu) and SARS-CoV-2 (the coronavirus) would be somewhere in the middle with the coronavirus likely being the lower of the two. The red curve tells us how many people will be vaccinated if everyone behaves completely rationally and out of self-interest alone. Notice that as the cost of infection increases (i.e. as the downside of getting infected grows) more people get vaccinated and the population gets closer and closer to the herd immunity threshold (black curve). Unfortunately, it never gets there! To make matters worse, when c is just slightly bigger than one, i.e. when people don’t think the virus is all that dangerous, the difference between what is best for society and what is best for the individual becomes quite pronounced. Put another way, if people act exclusively out of self-interest, then we all end up worse off.
It is worth emphasizing that this is not a scenario where getting vaccinated makes you worse off. As long as c>1, getting vaccinated is better than getting sick. The problem is just that letting other people getting vaccinated so you don’t have to is better still. This poses a conundrum. How can we overcome the free rider problem to achieve the best outcome, given that homo economicus cannot be trusted to achieve it? There are a few possible solutions:
1. People could be forced to get vaccinated. This would achieve the goal of producing herd immunity, but at what cost? Is it appropriate to the government to do such things? I suspect that most would argue that this is not an appealing option.
2. People could be incentivized to get vaccinated. That is the approach used for most infectious diseases these days. People are not required to be vaccinated for chicken pox, measles, etc. per se, but certain public goods such as public education may be unavailable to those who have not been vaccinated. That said, this sort of approach would be difficult to implement with the urgency required for addressing an ongoing pandemic such as COVID-19. Paying people to get vaccinated would probably do the trick, but that might lead to a host of unintended and undesirable consequences (such as decreased willingness to be accept other vaccinations without compensation).
3. People could be asked to get vaccinated for the good of their fellow man. Appeals to altruism would be ineffective with homo economicus, but they just might work with homo sapiens. I expect that once a promising COVID-19 vaccine gets close to the finish line, PR efforts to persuade people to get vaccinated will greatly intensify.
The question we should all be asking ourselves is, when the time comes will we be willing to get vaccinated? I know quite a few people who believe that “because they are pushing vaccines so hard, they can’t be trusted”. However, my hope in writing this post is that some might recognize that:
Widespread vaccination is likely the fastest and safest path to herd immunity.
Although some concern about the safety of a new vaccine is warranted, there are plenty of reasons to expect that should a vaccine make it through clinical trials and receive FDA approval, it will be much safer than taking your chances with the virus.
Although it is rational to want to be the free rider who benefits from the safety that herd immunity provides without the cost of vaccination, if everyone were to behave that way we would all be worse off.
Efforts to persuade people to get vaccinated are not necessarily evidence of some malicious scheme for controlling you and making a profit, they are a logical and necessary step to overcome the gap between the optimal vaccination rate for society and the likely outcome if people behave out of self-interest.
Before, concluding it is worth revisiting the question from the beginning of the post. “What is man?” I would argue that although homo economicus may be a useful model for human behavior, it has its limitations. In circumstances like this, I hope that we will be more than homo economicus. I hope that we will act not out of self-interest, but out of concern for one another. As I weigh the decision of whether to get vaccinated or not, the words of Philippians 2:3-4 weigh heavily on my mind:
“Do nothing from selfish ambition or conceit, but in humility count others more significant than yourselves. Let each of you look not only to his own interests, but also to the interests of others.”
As a Christian, I am called to consider the needs of others above my own. The reason for this is that God himself cares for the well-being of man (as David noted in the aforementioned psalm), so caring for others is a natural response to those who love him. This means that as a Christian, I should be willing to do what is best for us, and not just what is best for me. In the context of vaccination, this means that I expect to be first in line, not because I am so concerned about getting COVID, after all I have the luxury of being low risk, but because it is the least that I can do to help all of us put this dark chapter behind us. I hope that some of you will join me.
PS. This is not to say that I will make that decision blindly, assuming a vaccine makes it that far. I expect to do my homework and read up on the results from clinical trials to make sure that it was tested properly and is indeed safe, but barring any unexpected problems I will not hesitate to be an early adopter.
PPS. If you are interested in the mathematical details involved in the game theoretic analysis of vaccination, check out this paper. The graph above is based on equation 2.2 from the paper. Note: I use a slightly different definition of c (the reciprocal of the one in the paper). In the plot, I use R0=2.5.



Comments