About those surges of COVID patients...
- Mark J. Panaggio
- Jul 14, 2020
- 10 min read
Back in March when the world shut down, hospitals began bracing themselves for an uncertain future. There were stories of hospitals in Italy and Spain that had been overrun by patients infected with the new virus. ICUs were overwhelmed and hospitals were running out of beds. When the same thing started happening in New York, hospitals around the country began to prepare for the worst. Elective procedures were canceled, and staff members were told to get ready for a surge. In a few places, like Detroit, these surges arrived with devastating force and hospitals were pushed to the limit, however in many other places, the surges failed to materialize. Without elective procedures, hospitals were unusually empty and many employees had their hours scaled back. Some hospitals even had to resort to layoffs just to remain afloat.
Naturally, many were angry about this turn of events. They felt that they had been lied to. They were told that surges were on their way and the surges did not come. Many used this to argue that the experts had all been wrong, and that we were overreacting to the virus. Even today, as case totals reach record levels and the death totals have begun to climb again, as hospitals in Texas, California, Florida and Arizona are dealing with droves of patients, many people still point to the surges that never came as evidence that epidemiologists are alarmists who cannot be trusted. These people are quick to dismiss the guidelines about wearing masks in public and avoiding large gatherings as paranoid overreactions of cowards (or worse).
So why didn’t the surges come as promised? And what does this tell us about what the future holds? In this post, I would like to take look at some of the math that explains why it is so difficult to predict when surges will hit, even if we can be confident that they will arrive eventually.
To set the stage, let’s consider a simple example of a random process: a repeated coin flip. For a normal coin, the probability that it comes up heads is 0.5, but let’s consider a hypothetical coin where the probability of obtaining heads is some number p that could in principle be much smaller than that. As long as p is greater than zero, it is inevitable that, if we continue to flip the coin, heads will eventually show up. However, if p is small, then we may need to flip coins for a while to see that happen. If p =0.1 (i.e. heads only comes up 10% of the time), then on average it will take 10 flips to get one heads. If p=0.01, then on average it will take 100 flips. In general, the expected number of flips required to get heads will be 1/p.
If obtaining heads represents some rare but undesirable event, then we might use this average number of trials (also known as the expected value) as a way to quantify risk. This is natural because, for the most part, people tend to have a good intuitive understanding of averages. If someone were to say that the average driver can expect to drive 200000 miles between car accidents, then it would be easy for most of us to recognize that driving is a relatively low risk event.
However, expected values are not the only thing worth considering when describing random processes in the context of risk. It is also important to consider the variance. Going back to the coin example, if p=0.1, the average number of flips it takes to get heads is 10, but it doesn’t always happen on the 10th flip. Sometimes it will happen sooner, and sometimes it will happen later. Variance tells us how wide the plausible range of values is. When p is large, this variance is relatively small. If you have a 90% chance of getting heads, then you can be pretty confident (there is a 99% chance) that heads is going to show up within the first two flips. So, there is very little uncertainty about when heads will appear. However, if p is small, then the uncertainty grows. We can see this by running an experiment (or better yet a simulation) where we flip weighted coins over and over and see how long it takes to for heads to appear. If p=0.1, then we need to wait 30 flips to have a 95% chance of observing heads.

For p=0.001, it takes over 300 flips.

In general, the variance is given by the equation (1-p)/p^2 which I have graphed below.
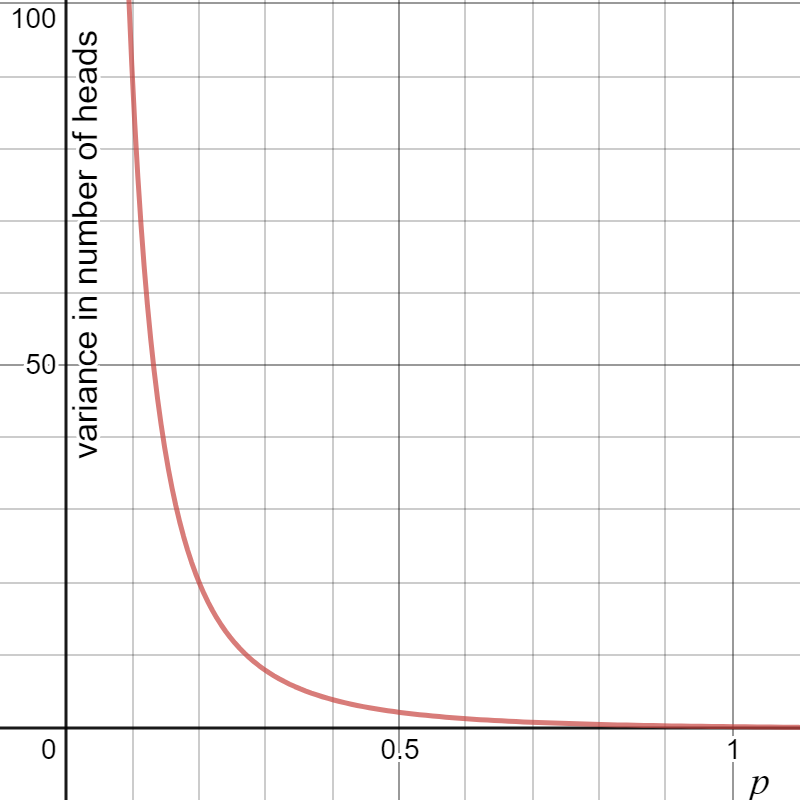
Notice that as p goes to zero, the variance gets larger and larger! In other words, when the event of interest is rare, our uncertainty about how long it will take for the event to happen goes up and up.
So what does this have to do with pandemics and hospital surges? Well think of flipping heads as a model for person to person spread of the novel coronavirus. During the early stages of an outbreak, there may only be one person who is sick, so the probability of an infectious event takes place is relatively small. This means that there is a great deal of uncertainty about how long it will take for the second person to get sick, and the third and so on. This means that early on, randomness has a big effect on how long it will take to go from one sick person to 100. The time this takes has a high degree of variance! However, as the number of sick people grows, the probability of infectious events grows and the uncertainty decreases making it easier to predict the timeline of an epidemic. Mathematical models for epidemics confirm this.
To illustrate this, I went back to the toy model for an epidemic in a small town that I discussed back in March (See https://markpanaggio.wixsite.com/home/post/what-happens-if-we-reopen-the-economy for details). This time I started with one sick patient and then ran 100 simulations to see (a) how long it took to go from 1 patient to 100 patients, and (b) how long it took to go from 101 patients to 200. Here are the key observations:
Takeaway #1: The first hundred infections take much longer than the second hundred. On average it took around 62 days to reach 100 cases, but less than 10 to go from 100 to 200.
Takeaway #2: The time it takes for the first hundred people to be infected varies a lot more than the second hundred. The standard deviation (which is the square root of the variance) of the number of days it took to reach 100 was around 18. This means that it was not unusual to see it take anywhere from 45 to 80 days to reach 100 cases. However, the standard deviation for the next 100 cases was around 2 days. In other words, once you hit 100 cases, you could be quite confident that you would cross 200 cases in 8 to 12 days.
All of this suggests that it can be quite difficult to predict how long it will take for an epidemic to get going, but once it does its time course can be quite predictable. In the context of surges, this means that it is much harder to know when the surge will hit than it is to know that it will hit eventually.
Takeaway #3: A few good/bad breaks early on make a big difference. Twenty-nine out of one hundred times the simulation never got past 100 infected people. With a little luck, the first couple of sick people got better before infecting anyone else and the outbreak fizzled out. This means the outbreak couldn’t happen until an outsider brought the virus back to the town (Which was not allowed in the simulation). So, when COVID-19 first arrives in an area, there is no guarantee that it will result in an outbreak.
Takeaway #4: Once the outbreak gets going, not much can stop it. Out of the 71 times that the simulation did reach 100 infections, it reached 200 patients every single time. In other words, the epidemic becomes much more predictable once it reaches critical mass. In a highly interconnected world, where people travel between communities, it is virtually impossible to prevent a virus that is as prevalent as the novel coronavirus from being introduced to a community. So, it may not be possible to prevent the first case. However, it is much easier to stop 1 case from turning into 100 than it is to stop 100 from turning into 200 or more.
All of this discussion neglects another important factor: social distancing. If people change their behavior (and the extent to which people will do that is quite difficult to predict!), then the uncertainty about when things will happen increases even more. If a population starts social distancing when there are a relatively small number of cases, then they have a good chance of being able to postpone or even avoid a large scale outbreak. That is precisely what many small towns around the country experienced. Places where a small number of cases were observed didn’t always turn into hotspots because people changed their behavior to slow the spread. As a result, the impending surge slowed to a trickle. In other words, the response likely PREVENTED the surges from taking place, at least temporarily. However, once people started returning to normal activities, the virus was again able to proliferate and quite a few places that avoided a significant surges in March and April are now experiencing surges in July.
The point is that hospitals were not wrong to prepare for surges, but some may have been wrong in their timing. It was probably not yet necessary to cancel elective procedures in places with few COVID cases, because the surge was still a long way off. Due to the large uncertainty that is present during the early stages of an epidemic, it can be difficult to predict precisely when the surge will arrive, so those decisions were likely made out of an abundance of caution.
Looking back, it is clear that if some of those hospitals had been able to continue normal operations, the economic hardship that they experienced might have been avoided. And that brings us to the last problem: testing. At that stage in the game, our country was woefully behind in monitoring the spread of the virus, so many governors, mayors and hospital administrators were forced to make decisions in the absence of reliable data. They had no way of knowing whether the pandemic had already reached critical mass in their area, and therefore whether the surge was imminent or a long way off, so they had to make their decisions blind. That makes for impossible decisions: If you react too early, you get ridiculed and dismissed as a reactionist and unnecessary economic hardship can occur, but if you react too late, there may be no way to avoid having your hospitals overrun. As a result, the people entrusted with these decisions had to make judgement calls, and they didn't always make the right ones. Some of the measures they took were premature and others were unnecessary, while still others saved hundreds if not thousands of lives.
Hindsight is 2020, and its easy to second guess the timing of those decisions now. Undoubtedly, mistakes were made, but that is not because epidemiologists got the pandemic all wrong. For the most part they have gotten that part right. Public policy is a different story. Predicting how people will respond to government recommendations and policies is much harder than predicting the spread of a virus. When you combine that with the inherent uncertainty involved in random processes (particularly those involving rare events) and with imperfect data about the current state of affairs, then choosing the right policy buttons to push and when to push them becomes incredibly difficult.
So, yes, some government officials and hospital administrators looked foolish in hindsight for preparing for a surge that did not arrive right way. But, perhaps instead of using that as an excuse to dismiss scientific expertise (and, let's be honest, the scientists and doctors warning us about the pandemic have rarely been the same people who were tasked with making the decisions), it would be better to take a second look at what is happening in many hospitals around the country right now. The surges were delayed, in large part due to the actions that we all took in March and April, but they are picking up steam now and unfortunately, in many parts of the country, this situation is worse than it ever got before.
I just finished reading a book (published in 2019!) called "Crisis in the Hot Zone", an account of the Ebola outbreak in West Africa that took place from 2014-2016 (I know...I am weird). Reading the conclusion and epilogue of the book during a global pandemic was a surreal experience and many of its conclusions seem very pertinent to our current existence. For example, when discussing the possibility of a future pandemic, the book cited Harvard biologist Pardis Sabeti who said:
“There’s not a lot of value in preparing for a war, because what happens in a war is unpredictable. But there is a lot of value in preparing for an outbreak, because what happens in an outbreak is predictable. Let’s be prepared, not scared.”
Sadly, even though the rising tide of COVID infections happening across the US was predictable, there are many who still dismiss the importance of preparation. They are unwilling to acknowledge the threat until it knocks at their door. Unfortunately, that is too late.
Let me conclude with a personal anecdote and one additional quote from the book. A couple weeks ago, one of my sons was using the bathroom. After urinating, he washed his hands before realizing that he had to go #2. After he finished, I reminded him to wash his hands, and his response was: "I already did before." At the time, I laughed and told him that he should do it again. But, now I realize that his nonsensical response was microcosm of what is going on in our country. We took precautions in March and April and they helped "flatten the curve", but now cases are spiking again and deaths are on the rise as well. To fail to take the relatively easy precautions now (like wearing masks and avoiding large indoor gatherings) just because "we already did that before" would be just as foolish and irresponsible.
If we want this to end or even to get under control, we need to continue fight even if it means take a step back for a time. The Ebola outbreak in Africa finally ended (but not before "three nations economies had functionally collapsed"). This is how some of the important players described its conclusion:
"What she saw in the Triangle [a particularly hard hit area in West Africa] was that the Kissi villages had started practicing reverse quarantine, closing themselves off from outsiders to prevent the virus from entering the village. This is exactly what villagers did at Yambuku in 1976. “The villagers were quarantining themselves at the local level."
“This is how all outbreaks end,” Armand Sprecher, the Doctors’ official in Brussels, said. “It’s always a change in behavior. Ebola outbreaks end when people decide they’re going to end.”
Africa is different from the US. The coronavirus is different from Ebola. Its mortality rate is over 50 times lower, and yet it has killed 50 times as many people because it is stealthier and harder to detect. Despite these differences I suspect that there are still lessons we can learn. Let's hope we will be willing to do that.



Comments